Size Robustness Analysis

Preparing data

Libraries

fpackage.check <- function(packages) { # (c) Jochem Tolsma
  lapply(packages, FUN = function(x) {
    if (!require(x, character.only = TRUE)) {
      install.packages(x, dependencies = TRUE)
      library(x, character.only = TRUE)
    }
  })
}
packages = c("tidyverse", "viridis", "kableExtra","ggridges", "viridis", "ggdark", "ggplot2", "patchwork", "sjPlot")
fpackage.check(packages)

Import the NSUM data and recreate the NSUM module.

#import nells file.
load(file = "data_analysis/data/data_processed/nells_data/2022-11-09_nells-nsum-prepped-data.rds")

Import the model estimates from the estimated NSUM models. I have choosen the model which uses Ibrahim for the ethnic names.

Main analysis results

if (file.exists(
  "data_analysis/results/nsum_output/main/combined_data/df_models_nsum_long.rds"
)) {
  load(file = "data_analysis/results/nsum_output/main/combined_data/df_models_nsum_long.rds")
} else {
  list_files <-
    as.list(
      dir(
        "data_analysis/results/nsum_output/main/model/",
        full.names = T
      )
    )
  #create loop lists
  kds <- list()
  kdssd <- list()
  data <- list()
  list_df <- list()
  
  #loop to extract information
  for (i in 1:length(list_files)) {
    #i = 1
    print(paste0("Number ", i, " of ", length(list_files)))
    load(list_files[[i]])
    kds[[i]] <-
      rowMeans(degree$d.values, na.rm = TRUE) # calculate rowmean of netsize iterations: so the retained chains
    kdssd[[i]] <-
      matrixStats::rowSds(degree$d.values) # calculate sd of 4k estimates per row: sd for those values
    data[[i]] <- cbind(kds[[i]], kdssd[[i]]) # combine them
    list_df[[i]] <-
      cbind(as_tibble(data[[i]]), nells_nsum$id) # add NELLS id variable
    strings <-
      str_split(str_extract(list_files[[i]][1], pattern = "estimates.+"),
                pattern = "_")  # add holdout number
    list_df[[i]] <- list_df[[i]] %>%
      mutate(
        holdout = as.numeric(str_extract(strings[[1]][2], pattern = "[[:digit:]]{1,}")))
  }
    #combine results and save
    df_models_nsum_long <- list_df %>%
      bind_rows() %>%
      rename(mean = V1,
             sd = V2,
             id = 3)
    #save image
    save(df_models_nsum_long, file = "data_analysis/results/nsum_output/main/combined_data/df_models_nsum_long.rds")
}

Holdout sensitivity analysis

In the estimation we need to set one of the known populations to missing. We will now check how sensitive variables ommission is for the network size estimate and see whether some groups are more sensitive to this than others.

First of all, create a table of median, mean, and the SD of network size for each unknown variable.

#create summary table
nsum_sum_long <- df_models_nsum_long %>%
  mutate(Unknown = factor(
    holdout,
    levels = 1:16,
    labels = c(
      "Daan",
      "Kevin",
      "Edwin",
      "Albert",
      "Emma",
      "Linda",
      "Ingrid",
      "Willemina",
      "Ibrahim",
      "Prison",
      "MBO",
      "HBO",
      "University",
      "Secundary education",
      "Owns second home",
      "Unemployed"
    )
  )) %>%
  group_by(Unknown) %>%
  summarise(
    Mean = mean(mean),
    Median = median(mean),
    SD = mean(sd),
    .groups = "drop"
  )

nsum_sum_long %>% 
  kbl() %>% 
  kable_paper(full_width = F,
              )

Unknown	Mean	Median	SD
Daan	935.0754	699.8811	337.5926
Kevin	969.7256	736.7016	351.2121
Edwin	1003.2393	766.4572	355.3362
Albert	1042.2279	788.9354	364.7517
Emma	960.7677	720.3704	340.0373
Linda	996.7474	765.4803	349.0902
Ingrid	1040.9216	800.1643	373.5502
Willemina	1023.1083	776.8069	361.9219
Ibrahim	803.5329	629.7463	265.5233
Prison	1035.6435	797.1834	369.2989
MBO	1025.8919	802.1888	352.6240
HBO	1035.5729	811.7983	358.5143
University	1018.8204	782.1697	349.7081
Secundary education	1034.6165	809.8754	361.0537
Owns second home	1025.6079	789.9623	357.7683
Unemployed	1034.3700	801.8969	363.9277

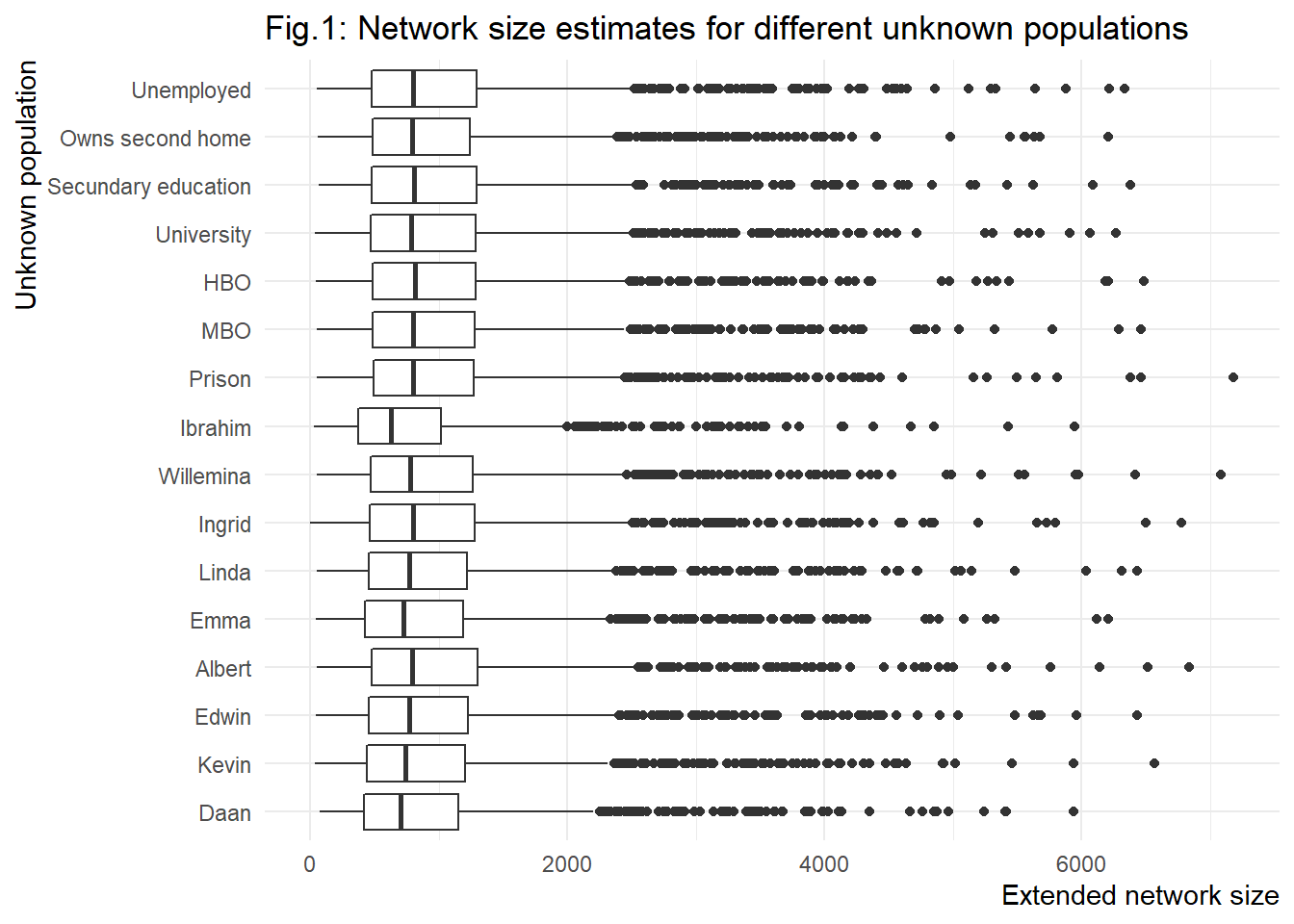
In mean network size there is realtively litte difference in the different size estimates with different unkown populations. The exception is when we set ibrahim to unknown, the mean and median size drops marekdly. Also, the median of network sizes is more sensitive than the mean network size. In the figure below, we show the differneces in boxplot which shows a similar pciture. Overall, bar the exception of Ibrahim, differences are small and neglible.

df_models_nsum_long %>%
  mutate(ommitted = factor(
    holdout,
    levels = 1:16,
    labels = c(
      "Daan",
      "Kevin",
      "Edwin",
      "Albert",
      "Emma",
      "Linda",
      "Ingrid",
      "Willemina",
      "Ibrahim",
      "Prison",
      "MBO",
      "HBO",
      "University",
      "Secundary education",
      "Owns second home",
      "Unemployed"
    )
  )) %>% 
  ggplot(aes(x = mean,
             y = ommitted)) +
  geom_boxplot(position = position_dodge(width = 1)) + 
  scale_fill_viridis_d(option = "D") +
  scale_color_viridis_d(option = "D") + 
  theme_minimal() +
  theme(legend.position = 'none',
        #plot.background = element_rect(fill = '#404040', colour = '#404040'),
        #panel.background = element_rect(fill = '#404040', colour = '#404040'),
        axis.title.y = element_text(hjust = 1),
        axis.title.x = element_text(hjust = 1),
        text = element_text(colour = "black"),
        strip.text = element_text(colour = "black")
        ) +
  labs(y = "Unknown population",
       x = "Extended network size",
       title = "Fig.1: Network size estimates for different unknown populations")

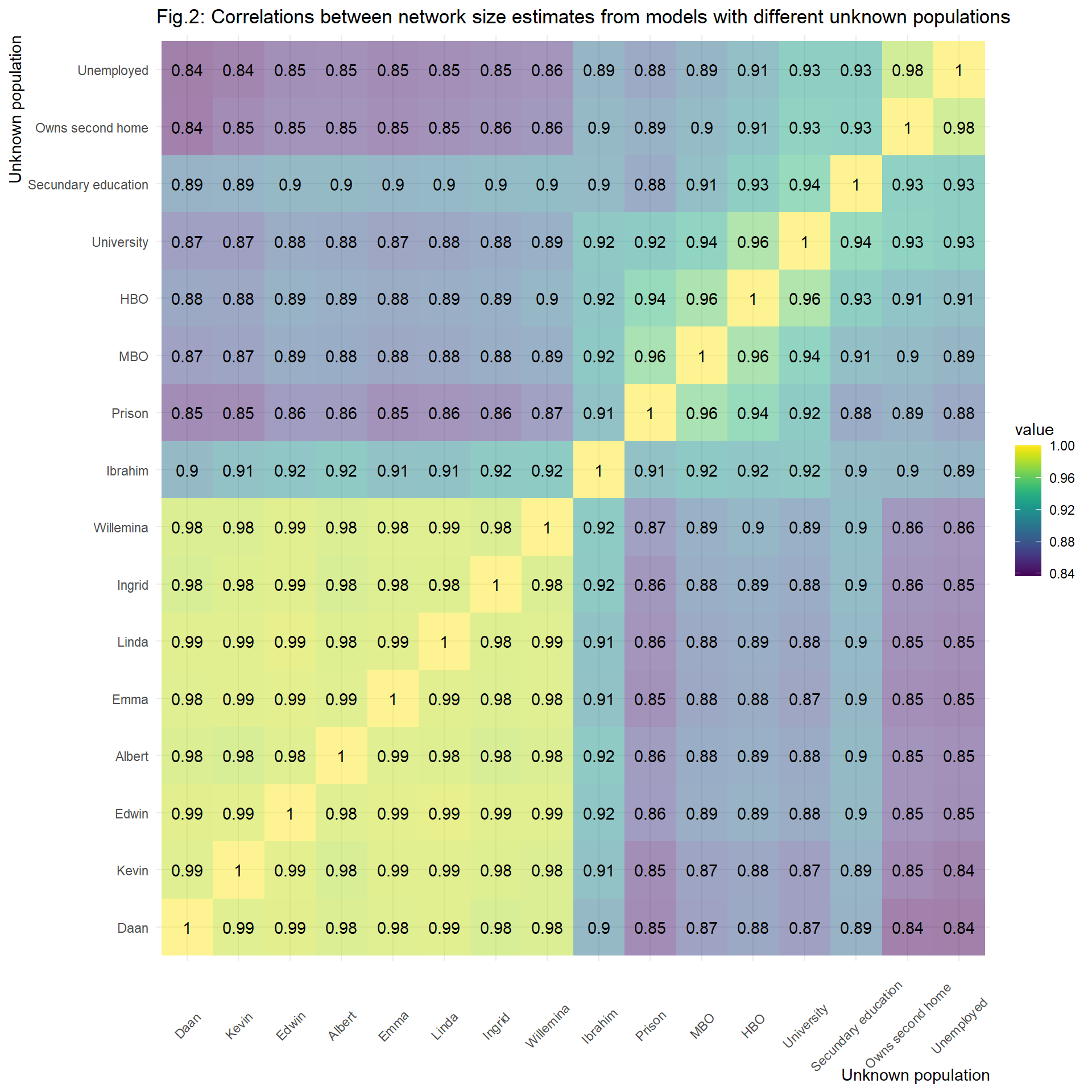
This only showed differences at the aggregate level. We also want to know whether these different size estimates are also robust on the individual. For this reason we created a correlation plot which shows the correlation between network size of the different unknown populations. OVerall these seem reliable ( r > 0.85), however, we find a discrepancy between names and categories. The within correlation between these is larger (~95) than the between these groups (~85).

#create wide file for correlation plot
df_models_nsum_wide <- df_models_nsum_long %>% 
  mutate(Ommitted = factor(
    holdout,
    levels = 1:16,
    labels = c(
      "Daan",
      "Kevin",
      "Edwin",
      "Albert",
      "Emma",
      "Linda",
      "Ingrid",
      "Willemina",
      "Ibrahim",
      "Prison",
      "MBO",
      "HBO",
      "University",
      "Secundary education",
      "Owns second home",
      "Unemployed"
    )
  )) %>% 
  arrange(id, Ommitted) %>% 
  select(-sd, -holdout) %>% 
  tidyr::pivot_wider(names_from = c(Ommitted),
              values_from = c(mean)) 

#create correlation file
cor_df <- df_models_nsum_wide %>% 
  select(-id) %>% 
  select(!contains("sd")) %>% 
  cor() %>% 
  as_tibble() %>% 
  mutate(variable_x = factor(1:16,
                             levels = 1:16,
                             labels = c(
      "Daan",
      "Kevin",
      "Edwin",
      "Albert",
      "Emma",
      "Linda",
      "Ingrid",
      "Willemina",
      "Ibrahim",
      "Prison",
      "MBO",
      "HBO",
      "University",
      "Secundary education",
      "Owns second home",
      "Unemployed"
    ))) %>% 
  tidyr::pivot_longer(1:16,
               names_to = "variable_y",
               values_to = "value")  %>% 
  mutate(variable_y = fct_relevel(variable_y,
                                  c(
      "Daan",
      "Kevin",
      "Edwin",
      "Albert",
      "Emma",
      "Linda",
      "Ingrid",
      "Willemina",
      "Ibrahim",
      "Prison",
      "MBO",
      "HBO",
      "University",
      "Secundary education",
      "Owns second home",
      "Unemployed"
    )))

#correlation plot
cor_df %>% 
  ggplot(aes(x = variable_x, y = variable_y, fill = value)) +
  geom_tile(alpha = 0.5) +
  geom_text(aes(label = round(value, 2))) +
  theme_minimal() +
  scale_fill_viridis(option = "D") + 
  theme(axis.text.x = element_text(angle = 45,
                                   vjust = 0.4),
        #plot.background = element_rect(fill = "#D4D9DE", colour = "#D4D9DE"),
        #panel.background = element_rect(fill ="#D4D9DE", colour = "#D4D9DE"),
        axis.title.y = element_text(hjust = 1),
        axis.title.x = element_text(hjust = 1),
        text = element_text(colour = "black"),
        strip.text = element_text(colour = "black")
        ) +
  labs(x = "Unknown population",
       y = "Unknown population",
       title = "Fig.2: Correlations between network size estimates from models with different unknown populations")

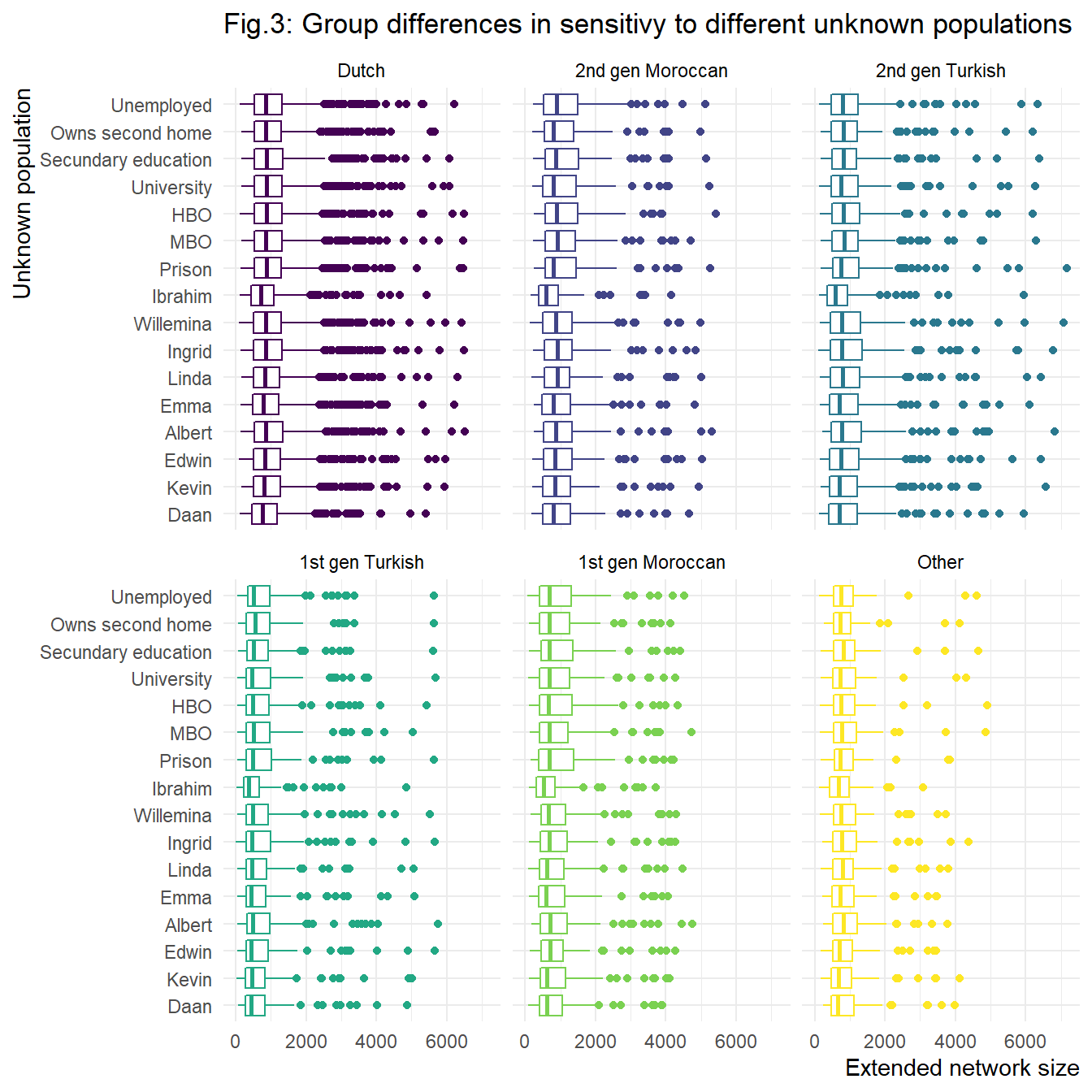
Since we are interested in group differences in network size, we would want to know whether groups differ in their sensitivity to different specifications of the main NSUM model. Based on the figure presented below, there are no major group differences bar Ibrahim.

nells_test_df <- df_models_nsum_long %>% 
  left_join(nells_nsum) 

nells_test_df %>% 
  mutate(ommitted = factor(holdout,
                           levels = 1:16,
                             labels = c(
      "Daan",
      "Kevin",
      "Edwin",
      "Albert",
      "Emma",
      "Linda",
      "Ingrid",
      "Willemina",
      "Ibrahim",
      "Prison",
      "MBO",
      "HBO",
      "University",
      "Secundary education",
      "Owns second home",
      "Unemployed"
    ))) %>% 
  ggplot(aes(x = mean,
             y = ommitted,
             color = migration_background_fac)) +
  geom_boxplot(position = position_dodge(width = 1)
               #,
               #fill = "#D4D9DE"
               ) +
  facet_wrap(vars(migration_background_fac)) +
  scale_fill_viridis_d(option = "D") +
  scale_color_viridis_d(option = "D") + 
  theme_minimal() +
  theme(legend.position = 'none',
        #plot.background = element_rect(fill = "#D4D9DE", colour = "#D4D9DE"),
        #panel.background = element_rect(fill ="#D4D9DE", colour = "#D4D9DE"),
        axis.title.y = element_text(hjust = 1),
        axis.title.x = element_text(hjust = 1),
        text = element_text(colour = "black"),
        strip.text = element_text(colour = "black")
        ) +
  labs(y = "Unknown population",
       x = "Extended network size",
       title = "Fig.3: Group differences in sensitivy to different unknown populations")

---

Copyright © 2024 Jeroense Thijmen