Analysis: figures and tables

Goal

Recreate results.

Set up and data import

#library
library(tidyverse)
library(lavaan)
library(data.table)
library(viridis)
library(foreach)

#data
load("results/riclpm/24-08-20_lavaan-moderation-results.Rdata")
load("results/riclpm/240816_lavaan-main-results.Rdata")

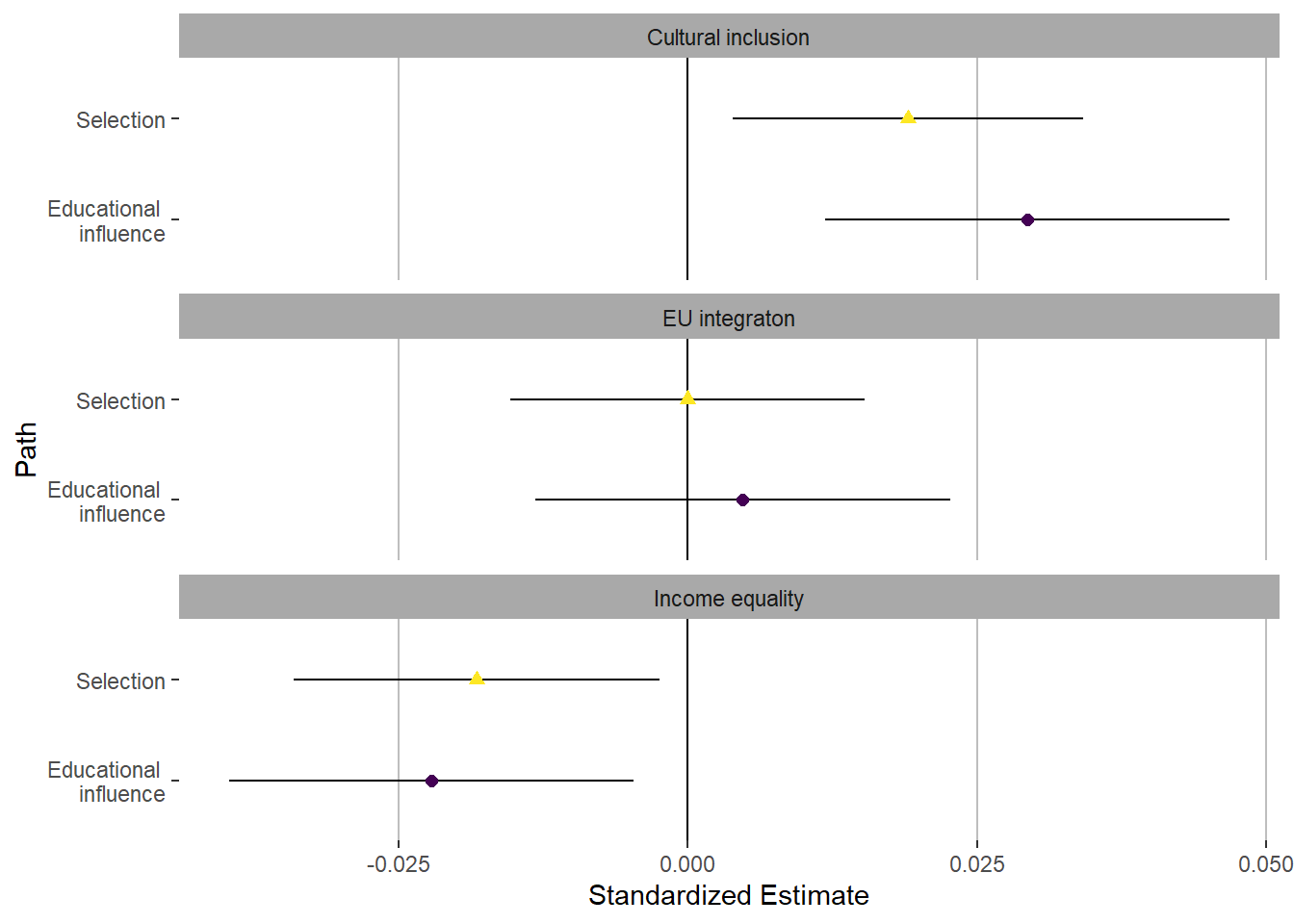
Main effects coefficient plot

Colour version

#extract standardized coefficients from models
coef_eu_m1 <- standardizedSolution(main_lavaan_results$`Main lavaan results`[[1]][[2]])
coef_cult_m1 <- standardizedSolution(main_lavaan_results$`Main lavaan results`[[2]][[2]])
coef_incdiff_m1 <- standardizedSolution(main_lavaan_results$`Main lavaan results`[[3]][[2]])

#select influence and selection coefficients
df_influence <- rbind(coef_cult_m1[68,], coef_eu_m1[68,], coef_incdiff_m1[68,])
df_selection <- rbind(coef_cult_m1[87,], coef_eu_m1[87,], coef_incdiff_m1[87,])
df_stability_att <- rbind(coef_cult_m1[67,], coef_eu_m1[67,], coef_incdiff_m1[67,])
df_stability_educ <- rbind(coef_cult_m1[88,], coef_eu_m1[88,], coef_incdiff_m1[88,])


#create list to store model dfs in
list_model <- list()

list_model[[1]] <- df_influence %>%
  select(lhs, rhs, est.std, se) %>%
  rename(dep_var = lhs, indep_var = rhs) %>%
  mutate(term = 3)

list_model[[2]] <- df_selection %>%
  select(lhs, rhs, est.std, se) %>%
  rename(dep_var = lhs, indep_var = rhs) %>%
  mutate(term = 2)

list_model[[3]] <- df_stability_att %>%
  select(lhs, rhs, est.std, se) %>%
  rename(dep_var = lhs, indep_var = rhs) %>%
  mutate(term = 1)

list_model[[4]] <- df_stability_educ %>%
  select(lhs, rhs, est.std, se) %>%
  rename(dep_var = lhs, indep_var = rhs) %>%
  mutate(term = 1)

#create coef plot
coef_plot_hypo1 <- list_model %>%
  rbindlist() %>%
  filter(term >1) %>%
  mutate(model = c(1,2,3,1,2,3),
         model = factor(model, labels = c("Cultural inclusion","EU integraton", "Income equality"), levels = 1:3),
         dep_var = ifelse(dep_var == "wcult_2", "Cultural Inclusion", dep_var),
         dep_var = ifelse(dep_var == "weu_2", "EU Integration", dep_var),
         dep_var = ifelse(dep_var == "wFeduc_a_2", "CDN Education", dep_var),
         dep_var = ifelse(dep_var == "winc_diff_2", "Income Equality", dep_var),
         term = factor(term, labels = c("Educational \n influence", "Selection"), levels = c(3,2))) %>%
  ggplot(aes(x = est.std, y = term, shape = term)) +
    geom_vline(xintercept = 0) +
  geom_linerange(aes(xmin = est.std - (se*1.96), xmax = est.std + (se*1.96)), position = position_dodge(width = 0.9)) +
  geom_point(aes(colour = term),
             position = position_dodge(width = 0.9), size = 2) +
  facet_wrap(vars(model), ncol = 1) +
  scale_colour_viridis(discrete = T,
                       option = "D")  +
  theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.y = element_blank(),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "none",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Path", x = "Standardized Estimate")

#save plot
ggsave(plot = coef_plot_hypo1, 
        file = "plots/results/riclpm_hypo1_coef_240924.eps",
        dpi = 600, 
       width = 5, 
       height = 4)

coef_plot_hypo1

Black and white version

#save bw version
coef_plot_hypo1_bw <- list_model %>%
  rbindlist() %>%
  filter(term >1) %>%
  mutate(model = c(1,2,3,1,2,3),
         model = factor(model, labels = c("Cultural inclusion","EU integraton", "Income equality"), levels = 1:3),
         dep_var = ifelse(dep_var == "wcult_2", "Cultural Inclusion", dep_var),
         dep_var = ifelse(dep_var == "weu_2", "EU Integration", dep_var),
         dep_var = ifelse(dep_var == "wFeduc_a_2", "CDN Education", dep_var),
         dep_var = ifelse(dep_var == "winc_diff_2", "Income Equality", dep_var),
         term = factor(term, labels = c("Educational \n influence", "Selection"), levels = c(3,2))) %>%
  ggplot(aes(x = est.std, y = term, shape = term)) +
    geom_vline(xintercept = 0) +
  geom_linerange(aes(xmin = est.std - (se*1.96), xmax = est.std + (se*1.96)), position = position_dodge(width = 0.9)) +
  geom_point(aes(colour = term),
             position = position_dodge(width = 0.9), size = 2) +
  facet_wrap(vars(model), ncol = 1) +
  scale_colour_grey()  +
  theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.y = element_blank(),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "none",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Path", x = "Standardized Estimate")

#save plot
ggsave(plot = coef_plot_hypo1_bw, 
        file = "plots/results/riclpm_hypo1_coef_bw_240924.eps",
        dpi = 600, 
       width = 5, 
       height = 4)


#export data for a table
 table1 <- list_model %>%
   rbindlist() 
 
 write_csv(table1, file = "output_raw/results/24-08-16_table1.csv")

#create coef plot for appendix
coef_plot_hypo1_appendix <- list_model %>%
  rbindlist() %>%
  filter(term >1) %>%
  mutate(model = c(1,2,3,1,2,3),
         model = factor(model, labels = c("Cultural inclusion","EU integraton", "Income equality"), levels = 1:3),
         dep_var = ifelse(dep_var == "wcult_2", "Cultural Inclusion", dep_var),
         dep_var = ifelse(dep_var == "weu_2", "EU Integration", dep_var),
         dep_var = ifelse(dep_var == "wFeduc_a_2", "CDN Education", dep_var),
         dep_var = ifelse(dep_var == "winc_diff_2", "Income Equality", dep_var),
         term = factor(term, labels = c("Educational \n influence", "Selection"), levels = c(3,2))) %>%
  ggplot(aes(x = est.std, y = term, shape = term)) +
    geom_vline(xintercept = 0) +
  geom_linerange(aes(xmin = est.std - (se*1.96), xmax = est.std + (se*1.96)), position = position_dodge(width = 0.9)) +
  geom_point(aes(colour = term),
             position = position_dodge(width = 0.9), size = 2) +
  facet_wrap(vars(model), ncol = 1) +
  scale_x_continuous(limits = c(-0.1, 0.1)) +
  scale_colour_viridis(discrete = T,
                       option = "D")  +
  theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.y = element_blank(),
        text = element_text(family = "sans", size = 12),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "none",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Path", x = "Standardized Estimate")
 
#save plot
ggsave(plot = coef_plot_hypo1_appendix, 
        file = "plots/results/coef_plot_hypo1_appendix.jpg",
        dpi = 600, width = 5, height = 4)

coef_plot_hypo1_bw

Extract fit measures

#create list with the m1 models
model_list_m1 <- list(main_lavaan_results$`Main lavaan results`[[1]][[2]],
                      main_lavaan_results$`Main lavaan results`[[2]][[2]],
                      main_lavaan_results$`Main lavaan results`[[3]][[2]]) 


#create result list
gof_extracted_m1 <-list()

#create loop to extract information
for (i in 1:length(model_list_m1)) { #i = EU_model6_unconstrained_groups_constrained_lag_fit
  fit_vector <- lavInspect(model_list_m1[[i]], what = "fit")
  
  fit_model <- fit_vector[c("rmsea", "tli", "cfi", "srmr", "bic", "aic", "chisq", "df")] %>%
    t() %>%
    as.data.frame() %>% 
    mutate(dep_var = c("EU-integration", 
                       "Cultural inclusion", 
                       "Income equality")[[i]])
  
  gof_extracted_m1[[i]] <- fit_model  
}

gof_extracted_m1 <- gof_extracted_m1 %>%
  rbindlist()

write_csv(gof_extracted_m1, file = "output_raw/results/24-08-16_gof_table_m1.csv")

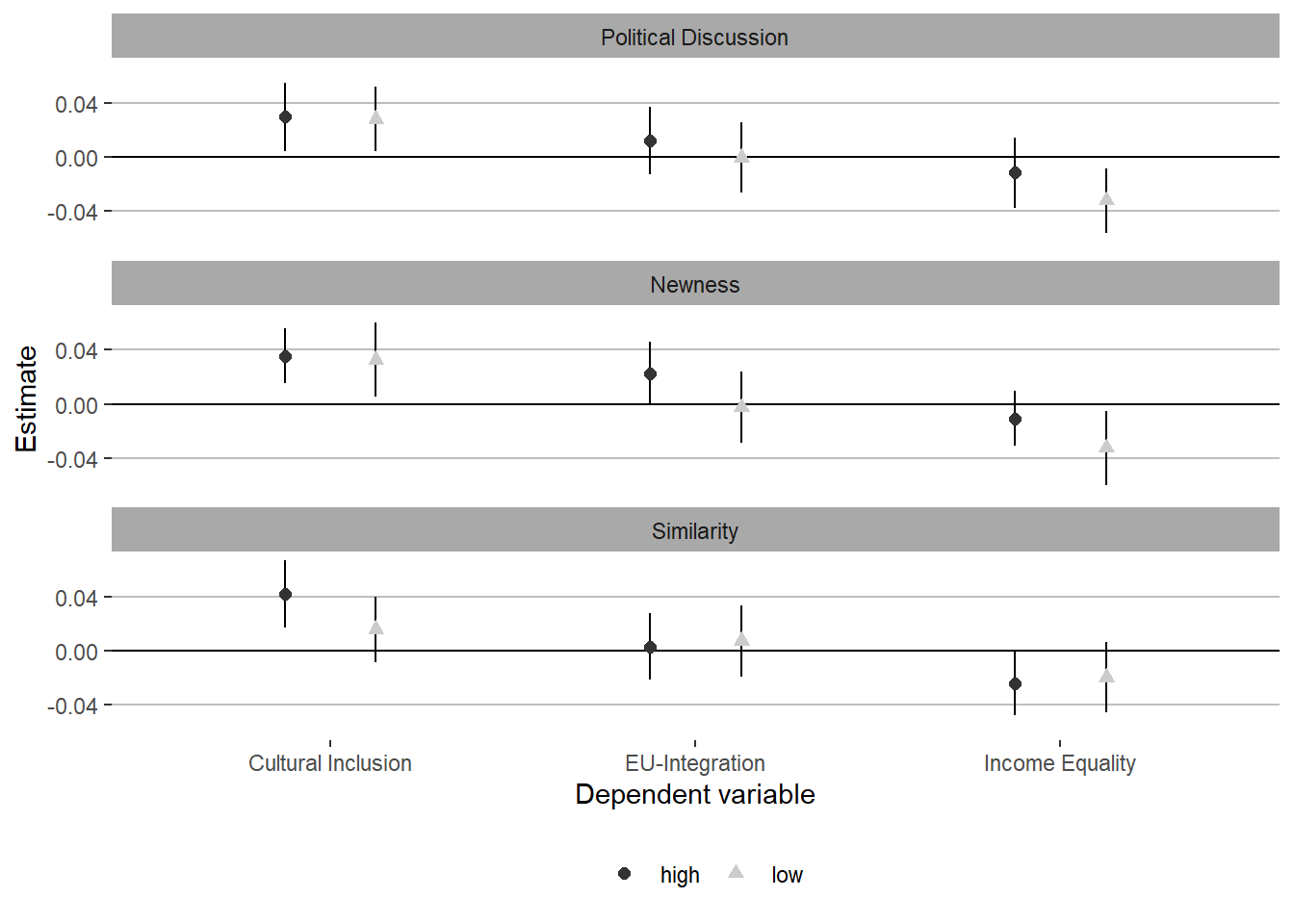
Moderation effects

Two groups

Colour version

coef_eu_m6 <- standardizedSolution(EU_model6_unconstrained_groups_constrained_lag_fit)
coef_cult_m6 <- standardizedSolution(cult_model6_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m6 <- standardizedSolution(inc_diff_model6_unconstrained_groups_constrained_lag_fit)

coefficients_m6 <- rbind(coef_eu_m6[c(68,282),], coef_cult_m6[c(68,282),], coef_incdiff_m6[c(68,282),]) %>%
  select(lhs, rhs, est.std, se)


list_model_between_two <- list()

list_model_between_two[[1]] <- coefficients_m6 %>%
  mutate(term = "Political Discussion",
         dep_var = c("EU-Integration","EU-Integration", "Cultural Inclusion",  "Cultural Inclusion", "Income Equality","Income Equality"),
         value = c("high", "low","high", "low","high", "low"))


## newness
coef_eu_m7 <- standardizedSolution(EU_model7_unconstrained_groups_constrained_lag_fit)
coef_cult_m7 <- standardizedSolution(cult_model7_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m7 <- standardizedSolution(inc_diff_model7_unconstrained_groups_constrained_lag_fit)

coefficients_m7 <- rbind(coef_eu_m7[c(63,260),], coef_cult_m7[c(63,260),], coef_incdiff_m7[c(63,260),]) %>%
  select(lhs, rhs, est.std, se)


list_model_between_two[[2]] <- coefficients_m7 %>%
  mutate(term = "Newness",
         dep_var = c("EU-Integration","EU-Integration", "Cultural Inclusion",  "Cultural Inclusion", "Income Equality","Income Equality"),
         value = c("high", "low","high", "low","high", "low"))

## similarity
coef_eu_m8 <- standardizedSolution(EU_model8_unconstrained_groups_constrained_lag_fit)
coef_cult_m8 <- standardizedSolution(cult_model8_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m8 <- standardizedSolution(inc_diff_model8_unconstrained_groups_constrained_lag_fit)

coefficients_m8 <- rbind(coef_eu_m8[c(68,282),], coef_cult_m8[c(68,282),], coef_incdiff_m8[c(68,282),]) %>%
  select(lhs, rhs, est.std, se)

list_model_between_two[[3]] <- coefficients_m8 %>%
  mutate(term = "Similarity",
         dep_var = c("EU-Integration","EU-Integration", "Cultural Inclusion",  "Cultural Inclusion", "Income Equality","Income Equality"),
         value = c("low", "high","low", "high","low", "high")) 

#create plot
coef_between_two <- list_model_between_two %>%
  rbindlist() %>%
  mutate(term = case_when(
    term == "Political Discussion" ~ 1,
    term == "Newness" ~ 2,
    term == "Similarity" ~ 3),
    term = factor(term, 
                  levels = 1:3,
                  labels = c(
                    "Political Discussion",
                    "Newness",
                    "Similarity"
                  ))) %>% 
  ggplot(aes(y = est.std, x = dep_var, shape = value)) +
  geom_hline(yintercept = 0) +
  geom_linerange(aes(ymin = est.std - (se*1.96), ymax = est.std + (se*1.96)),
                 position = position_dodge(width = 0.5)) +
    geom_point(aes(colour = value),
             position = position_dodge(width = 0.5), size = 2) +
  scale_colour_viridis(discrete = T,
                       option = "D") +
  facet_wrap(vars(term), ncol = 1) +
   theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.x = element_blank(),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Estimate", x = "Dependent variable")

coef_between_two

#extract plot
#to eps
ggsave(filename = "plots/results/riclpm_mod_coef_240820.eps",
       plot = coef_between_two,
       dpi = 600, 
       width = 5, 
       height = 5)


#export data for table two
table2 <- list_model_between_two %>%
  rbindlist()

write_csv(table2, file = "output_raw/results/2024-08-20_table2.csv")

Black and white version

# black and white plot
#create plot
coef_between_two_bw <- list_model_between_two %>%
  rbindlist() %>%
  mutate(term = case_when(
    term == "Political Discussion" ~ 1,
    term == "Newness" ~ 2,
    term == "Similarity" ~ 3),
    term = factor(term, 
                  levels = 1:3,
                  labels = c(
                    "Political Discussion",
                    "Newness",
                    "Similarity"
                  ))) %>% 
  ggplot(aes(y = est.std, x = dep_var, shape = value)) +
  geom_hline(yintercept = 0) +
  geom_linerange(aes(ymin = est.std - (se*1.96), ymax = est.std + (se*1.96)),
                 position = position_dodge(width = 0.5)) +
    geom_point(aes(colour = value),
             position = position_dodge(width = 0.5), size = 2) +
  scale_colour_grey() +
  facet_wrap(vars(term), ncol = 1) +
   theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.x = element_blank(),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Estimate", x = "Dependent variable")

coef_between_two_bw

#extract plot
#to eps
ggsave(filename = "plots/results/riclpm_mod_coef_bw_240820.eps",
       plot = coef_between_two_bw,
       dpi = 600, 
       width = 5, 
       height = 5)

GOF stat table

if(!file.exists("output_raw/results/2024-08-20_gof_table2.csv")){
gof_list <- list(EU_model6_unconstrained_groups_constrained_lag_fit,
                 cult_model6_unconstrained_groups_constrained_lag_fit,
                 inc_diff_model6_unconstrained_groups_constrained_lag_fit,
                 EU_model7_unconstrained_groups_constrained_lag_fit,
                 cult_model7_unconstrained_groups_constrained_lag_fit,
                 inc_diff_model7_unconstrained_groups_constrained_lag_fit,
                 EU_model8_unconstrained_groups_constrained_lag_fit,
                 cult_model8_unconstrained_groups_constrained_lag_fit,
                 inc_diff_model8_unconstrained_groups_constrained_lag_fit)

gof_extracted <- list()

for (i in 1:length(gof_list)) { #i = EU_model6_unconstrained_groups_constrained_lag_fit
  fit_vector <- lavInspect(gof_list[[i]], what = "fit")
  
  fit_model <- fit_vector[c("rmsea", "tli", "cfi", "srmr", "bic", "aic", "chisq", "df")] %>%
    t() %>%
    as.data.frame()
  
  gof_extracted[[i]] <- fit_model  
}

gof_extracted <- gof_extracted %>%
  rbindlist()

write_csv(gof_extracted, file = "output_raw/results/2024-08-20_gof_table2.csv")
} else{
  gof_extracted <- read.csv("output_raw/results/2024-08-20_gof_table2.csv")
}

Likelihood Ratio Test table

anova_list <- list()

#export anova results
anova_list[[1]] <- lavTestLRT(EU_model6_unconstrained_groups_constrained_lag_fit, EU_model6_constrained_lag_groups_fit)

anova_list[[2]] <- lavTestLRT(cult_model6_unconstrained_groups_constrained_lag_fit, cult_model6_constrained_lag_groups_fit)

anova_list[[3]] <- lavTestLRT(inc_diff_model6_unconstrained_groups_constrained_lag_fit, inc_diff_model6_constrained_lag_groups_fit)

anova_list[[4]] <- lavTestLRT(EU_model7_unconstrained_groups_constrained_lag_fit, EU_model7_constrained_lag_groups_fit)

anova_list[[5]] <- lavTestLRT(cult_model7_unconstrained_groups_constrained_lag_fit, cult_model7_constrained_lag_groups_fit)

anova_list[[6]] <- lavTestLRT(inc_diff_model7_unconstrained_groups_constrained_lag_fit, inc_diff_model7_constrained_lag_groups_fit)

anova_list[[7]] <- lavTestLRT(EU_model8_unconstrained_groups_constrained_lag_fit, EU_model8_constrained_lag_groups_fit)

anova_list[[8]] <- lavTestLRT(cult_model8_unconstrained_groups_constrained_lag_fit, cult_model8_constrained_lag_groups_fit)

anova_list[[9]] <- lavTestLRT(inc_diff_model8_unconstrained_groups_constrained_lag_fit, inc_diff_model8_constrained_lag_groups_fit)


anova_results <- anova_list %>%
  rbindlist()

write_csv(anova_results, "output_raw/results/2024-08-20_anova_table2.csv")

Descriptive statistics table

#create descriptive table
desstats <- MyData %>%
  select(starts_with("eu_"),
         matches("^cult_[[:digit:]]"),
         starts_with("inc_dif"),
         starts_with("Feduc"),
         starts_with("Fave"),
         starts_with("Fpol"),
         starts_with("Fsim"),
         starts_with("Frl"),
         starts_with("between_")) %>% 
  psych::describe() %>% 
  select(-1, -trimmed, -mad, -se) %>%
  round(.,3) %>%
  mutate(Variables = rownames(.)) %>% 
  tibble() %>% 
  select(10, 1:9)


write_csv(desstats, file = "output_raw/results/2023-08-20_desstats_table.csv")

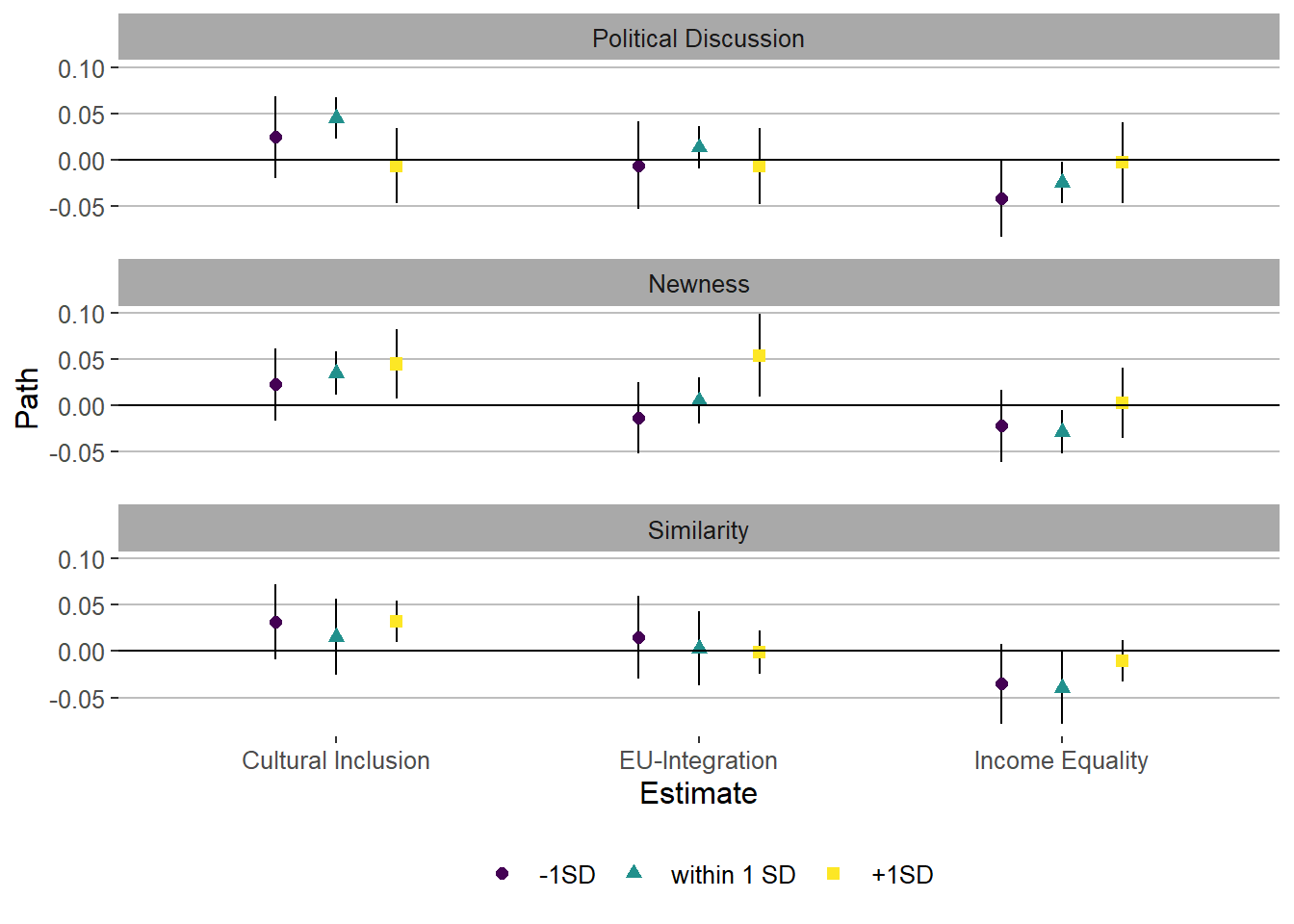
Robustness

Three groups

#Political discussion coefficients
coef_eu_m12 <- standardizedSolution(EU_model12_unconstrained_groups_constrained_lag_fit)
coef_cult_m12 <- standardizedSolution(cult_model12_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m12 <- standardizedSolution(inc_diff_model12_unconstrained_groups_constrained_lag_fit)

#extract coefficients from model
coefficients_m12 <-
  rbind(
    coef_eu_m12[c(68, 282, 496), ], 
    coef_cult_m12[c(68, 282, 496), ], 
    coef_incdiff_m12[c(68, 282, 496), ]
    ) %>%
  select(lhs, rhs, est.std, se)


#create list to store information
list_model_between_three <- list()

#store political discussion information
list_model_between_three[[1]] <- coefficients_m12 %>%
  mutate(
    term = "Political Discussion",
    dep_var = c(
      rep("EU-Integration", 3),
      rep("Cultural Inclusion", 3),
      rep("Income Equality", 3)
    ),
    value = rep(c(3:1)
                , 3)
  )

#Newness coefficients
coef_eu_m13 <- standardizedSolution(EU_model13_unconstrained_groups_constrained_lag_fit)
coef_cult_m13 <- standardizedSolution(cult_model13_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m13 <- standardizedSolution(inc_diff_model13_unconstrained_groups_constrained_lag_fit)

#extract coefficients from model
coefficients_m13 <-
  rbind(
    coef_eu_m13[c(63, 260, 457), ], 
    coef_cult_m13[c(63, 260, 457), ], 
    coef_incdiff_m13[c(63, 260, 457), ]
    ) %>%
  select(lhs, rhs, est.std, se)

#store political discussion information
list_model_between_three[[2]] <- coefficients_m13 %>%
  mutate(
    term = "Newness",
    dep_var = c(
      rep("EU-Integration", 3),
      rep("Cultural Inclusion", 3),
      rep("Income Equality", 3)
    ),
    value = rep(c(3:1)
                , 3)
  )

## Similarity coefficients
coef_eu_m14 <- standardizedSolution(EU_model14_unconstrained_groups_constrained_lag_fit)
coef_cult_m14 <- standardizedSolution(cult_model14_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m14 <- standardizedSolution(inc_diff_model14_unconstrained_groups_constrained_lag_fit)

#extract coefficients from model
coefficients_m14 <-
  rbind(
    coef_eu_m14[c(68, 282, 496), ], 
    coef_cult_m14[c(68, 282, 496), ], 
    coef_incdiff_m14[c(68, 282, 496), ]
    ) %>%
  select(lhs, rhs, est.std, se)

#store political discussion information
list_model_between_three[[3]] <- coefficients_m14 %>%
  mutate(
    term = "Similarity",
    dep_var = c(
      rep("EU-Integration", 3),
      rep("Cultural Inclusion", 3),
      rep("Income Equality", 3)
    ),
    value = rep(c(3:1)
                , 3)
  )

#create plot
coef_between_three <- list_model_between_three %>%
  rbindlist() %>%
  mutate(value = factor(value,
                        levels = 3:1,
                        labels = c("+1SD",
                  "within 1 SD",
                  "-1SD"))) %>% 
    mutate(term = case_when(
    term == "Political Discussion" ~ 1,
    term == "Newness" ~ 2,
    term == "Similarity" ~ 3),
    term = factor(term, 
                  levels = 1:3,
                  labels = c(
                    "Political Discussion",
                    "Newness",
                    "Similarity"
                  ))) %>%
  ggplot(aes(y = est.std, x = dep_var, shape = fct_rev(value))) +
  geom_linerange(aes(ymin = est.std - (se*1.96), ymax = est.std + (se*1.96)), position = position_dodge(width = 0.5)) +
    geom_point(aes(colour = fct_rev(value)),
             position = position_dodge(width = 0.5), size = 2) +
  geom_hline(yintercept = 0) +
  scale_colour_viridis(discrete = T,
                       option = "D") +
  facet_wrap(vars(term), ncol = 1) +
   theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.x = element_blank(),
        text = element_text(family = "sans", size = 12),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Path", x = "Estimate")

coef_between_three

#to jpg
ggsave(filename = "plots/results/riclpm_mod_coef_three_240820.pdf",
       plot = coef_between_three,
       dpi = 600, 
       width = 6, 
       height = 5)

Four groups

#Political discussion coefficients
coef_eu_m9 <- standardizedSolution(EU_model9_unconstrained_groups_constrained_lag_fit)
coef_cult_m9 <- standardizedSolution(cult_model9_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m9 <- standardizedSolution(inc_diff_model9_unconstrained_groups_constrained_lag_fit)

#extract coefficients from model
coefficients_m9 <-
  rbind(
    coef_eu_m9[c(68, 282, 496, 710), ], 
    coef_cult_m9[c(68, 282, 496, 710), ], 
    coef_incdiff_m9[c(68, 282, 496, 710), ]
    ) %>%
  select(lhs, rhs, est.std, se)


#create list to store information
list_model_between_four <- list()

#store political discussion information
list_model_between_four[[1]] <- coefficients_m9 %>%
  mutate(
    term = "Political Discussion",
    dep_var = c(
      rep("EU-Integration", 4),
      rep("Cultural Inclusion", 4),
      rep("Income Equality", 4)
    ),
    value = rep(c("4",
                  "3",
                  "2",
                  "1")
                , 3)
  )

#Newness coefficients
coef_eu_m10 <- standardizedSolution(EU_model10_unconstrained_groups_constrained_lag_fit)
coef_cult_m10 <- standardizedSolution(cult_model10_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m10 <- standardizedSolution(inc_diff_model10_unconstrained_groups_constrained_lag_fit)

#extract coefficients from model
coefficients_m10 <-
  rbind(
    coef_eu_m10[c(63, 260, 457, 654), ], 
    coef_cult_m10[c(63, 260, 457, 654), ], 
    coef_incdiff_m10[c(63, 260, 457, 654), ]
    ) %>%
  select(lhs, rhs, est.std, se)

#store political discussion information
list_model_between_four[[2]] <- coefficients_m10 %>%
  mutate(
    term = "Newness",
    dep_var = c(
      rep("EU-Integration", 4),
      rep("Cultural Inclusion", 4),
      rep("Income Equality", 4)
    ),
    value = rep(c("4",
                  "3",
                  "2",
                  "1")
                , 3)
  )

## Similarity coefficients
coef_eu_m11 <- standardizedSolution(EU_model11_unconstrained_groups_constrained_lag_fit)
coef_cult_m11 <- standardizedSolution(cult_model11_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m11 <- standardizedSolution(inc_diff_model11_unconstrained_groups_constrained_lag_fit)

#extract coefficients from model
coefficients_m11 <-
  rbind(
    coef_eu_m11[c(68, 282, 496, 710), ], 
    coef_cult_m11[c(68, 282, 496, 710), ], 
    coef_incdiff_m11[c(68, 282, 496, 710), ]
    ) %>%
  select(lhs, rhs, est.std, se)

#store political discussion information
list_model_between_four[[3]] <- coefficients_m11 %>%
  mutate(
    term = "Similarity",
    dep_var = c(
      rep("EU-Integration", 4),
      rep("Cultural Inclusion", 4),
      rep("Income Equality", 4)
    ),
    value = rep(c("4",
                  "3",
                  "2",
                  "1")
                , 3)
  )

#create plot
coef_between_four <- list_model_between_four %>%
  rbindlist() %>%
    mutate(term = case_when(
    term == "Political Discussion" ~ 1,
    term == "Newness" ~ 2,
    term == "Similarity" ~ 3),
    term = factor(term, 
                  levels = 1:3,
                  labels = c(
                    "Political Discussion",
                    "Newness",
                    "Similarity"
                  ))) %>%
  ggplot(aes(y = est.std, x = dep_var, shape = value)) +
  geom_linerange(aes(ymin = est.std - (se*1.96), ymax = est.std + (se*1.96)), position = position_dodge(width = 0.5)) +
    geom_point(aes(colour = value),
             position = position_dodge(width = 0.5), size = 2) +
  geom_hline(yintercept = 0) +
  scale_colour_viridis(discrete = T,
                       option = "D") +
  facet_wrap(vars(term), ncol = 1) +
   theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.x = element_blank(),
        text = element_text(family = "sans", size = 12),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Path", x = "Estimate")

coef_between_four

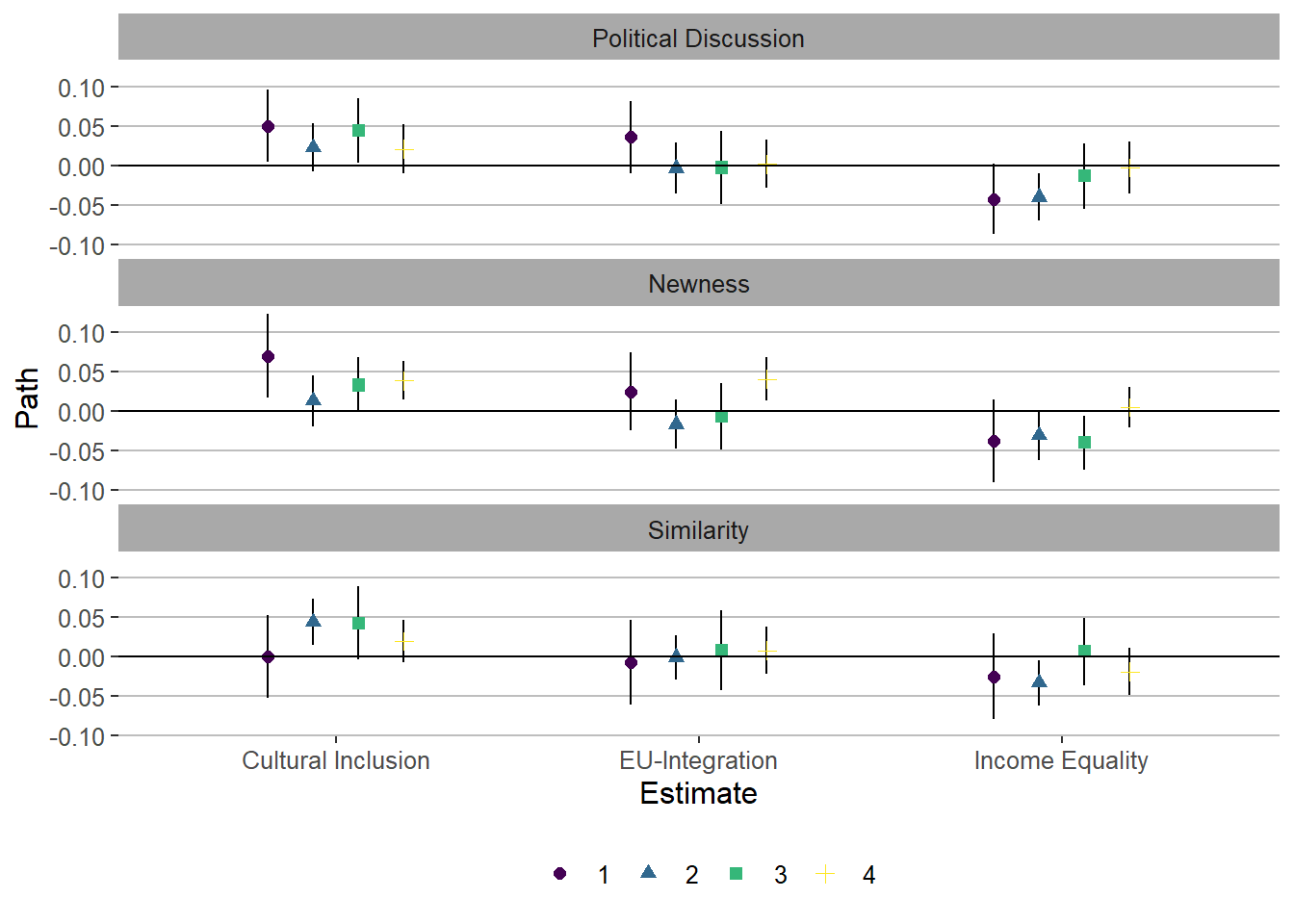
ggsave(filename = "plots/results/riclpm_mod_coef_four_240820.pdf",
       plot = coef_between_four,
       dpi = 600, 
       width = 6, 
       height = 5)

LISS length variable

coef_eu_m16 <- standardizedSolution(EU_model16_unconstrained_groups_constrained_lag_fit)
coef_cult_m16 <- standardizedSolution(cult_model16_unconstrained_groups_constrained_lag_fit)
coef_incdiff_m16 <- standardizedSolution(inc_diff_model16_unconstrained_groups_constrained_lag_fit)

coefficients_m16 <- rbind(coef_eu_m16[c(63,260),], coef_cult_m16[c(63,260),], coef_incdiff_m16[c(63,260),]) %>%
  select(lhs, rhs, est.std, se) %>%
  mutate(term = "Relationship Length",
         dep_var = c("EU-Integration","EU-Integration", "Cultural Inclusion",  "Cultural Inclusion", "Income Equality","Income Equality"),
         value = c("low","high", "low","high", "low","high"))

#create plot
coef_between_two_robnewness <- coefficients_m16 %>%
  ggplot(aes(y = est.std, x = dep_var, shape = value)) +
  geom_hline(yintercept = 0) +
  geom_linerange(aes(ymin = est.std - (se*1.96), ymax = est.std + (se*1.96)),
                 position = position_dodge(width = 0.5)) +
    geom_point(aes(colour = value),
             position = position_dodge(width = 0.5), size = 2) +
  scale_colour_viridis(discrete = T,
                       option = "D") +
  facet_wrap(vars(term), ncol = 1) +
   theme(panel.background = element_rect(fill = "#FFFFFF"),
        plot.background = element_rect(fill = "#FFFFFF"),
        panel.grid = element_line(colour = "grey"),
        panel.grid.major.x = element_blank(),
        text = element_text(family = "sans", size = 12),
        strip.background = element_rect(fill = "#A9A9A9"),
        panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        legend.background = element_rect(fill = "#FFFFFF"),
        legend.key = element_rect(fill = "#FFFFFF")) +
  labs(y = "Estimate", x = "Dependent variable")

coef_between_two_robnewness

#extract plot
#to jpg
ggsave(filename = "plots/results/riclpm_mod_robnew_coef_240820.jpg",plot = coef_between_two, dpi = 600, width = 4, height = 4)

---

Copyright © 2024 Jeroense Thijmen