Descriptive statistics

Descriptive statistics

Goal of this script is to show how to recreate the different tables and graphs in our paper.

Set up

Packages

#library
library(tidyverse)
library(data.table)
library(kableExtra)
library(patchwork)
library(ggpubr)
library(lme4)
library(viridis)
library(survival)
library(broom)
library(ggthemes)

Import

#load prepared data.
load("datafiles/data-processed/disaggregated_data/2022-06-13_dyad-survival-data-imputed.rda")

MyData <- nonkin_survival_data_lead_dependent_imputed

#change scientific notation
options(scipen = 999)

#rename dropped_lead into dropped, so we can easily repreoduce this code.
MyData <- MyData %>% 
  rename(dropped = dropped_lead)

#last dataprep
MyData <- MyData %>%
  mutate(
    educ_ego = educ_ego - 4,
    age = leeftijd - 15,
    age_sq = age * age,
    age_alter = age_alter - 1,
    educ_alter = educ_alter - 4,
    length_rel_member = length_rel_member - 1,
    length_rel_total = length_rel_total - 1,
    size = size - 1,
    ei_alter_gender_rev = (2 - (MyData$ei_alter_gender + 1)) - 1,
    ei_alter_ethnicity_rev = (2 - (MyData$ei_alter_ethnicity + 1)) - 1,
    origin_rec_nar = ifelse(is.na(origin_rec_nar), 3, origin_rec_nar),
    origin_rec_nar_fac = factor(
      origin_rec_nar,
      levels = 0:3,
      labels = c("None", "Non-western", "Western", "Missing")
    ),
    origin_alter_rec = ifelse(is.na(origin_alter_rec), 3, origin_alter_rec),
    origin_alter_rec_fac = factor(
      origin_alter_rec,
      levels = 0:3,
      labels = c("None", "Non-western", "Western", "Missing")
    ),
    length = ifelse(is.na(length), 4, length),
    length_fac = factor(
      length,
      levels = 1:4,
      labels = c("< 3 years",
                 "3 - 6 years",
                 "> 6 years", 
                 "Length missing")
      )
    )

#scale variables for me models
MyData <- MyData %>% 
  mutate(avsim_alter_educ_cen = scale(avsim_alter_educ),
         avsim_alter_age_cen = scale(avsim_alter_age),
         ei_alter_gender_rev_cen = scale(ei_alter_gender_rev),
         ei_alter_ethnicity_rev_cen = scale(ei_alter_ethnicity_rev),
         length_rel_member_cen = scale(length_rel_member),
         length_rel_total_cen = scale(length_rel_total),
         size_cen = scale(size),
         degree_cen = scale(degree))

Descriptive statistics

Descriptive statistics table

Full descriptive statistics table of the variables in the final sample as used in the paper.

#create descriptive statistics table
desstats_table <- MyData %>%
  mutate(
    no_mig = ifelse(origin_rec_nar == 0, 1, 0),
    nonwestern_mig = ifelse(origin_rec_nar == 1, 1, 0),
    western_mig =  ifelse(origin_rec_nar == 2, 1, 0),
    no_mig_a =  ifelse(origin_alter_rec == 0, 1, 0),
    nonwestern_mig_a =  ifelse(origin_alter_rec == 1, 1, 0),
    western_mig_a =  ifelse(origin_alter_rec == 2, 1, 0),
    rel_a_b3 = ifelse(length == 1, 1, 0),
    rel_a_36 = ifelse(length == 2, 1, 0),
    rel_a_o6 = ifelse(length == 3, 1, 0),
    rel_missing = ifelse(is.na(length), 1, 0),
    partner_fam = ifelse(as.numeric(rel_alter_rec) == 1, 1, 0),
    closefam = ifelse(as.numeric(rel_alter_rec) == 2, 1, 0),
    otherfam = ifelse(as.numeric(rel_alter_rec) == 3, 1, 0),
    coll = ifelse(as.numeric(rel_alter_rec) == 4, 1, 0),
    samegroup = ifelse(as.numeric(rel_alter_rec) == 5, 1, 0),
    neighbour = ifelse(as.numeric(rel_alter_rec) == 6, 1, 0),
    friend = ifelse(as.numeric(rel_alter_rec) == 7, 1, 0),
    advisor = ifelse(as.numeric(rel_alter_rec) == 8, 1, 0),
    otherrel = ifelse(as.numeric(rel_alter_rec) == 9, 1, 0),
    not_dear = ifelse(as.numeric(dear_alter_rec) == 0, 1, 0),
    dear = ifelse(as.numeric(dear_alter_rec) == 1, 1, 0),
    not_asked = ifelse(as.numeric(dear_alter_rec) == 2, 1, 0),
    not_divorced = ifelse(as.numeric(divorced_fac) == 1, 1, 0),
    divorced = ifelse(as.numeric(divorced_fac) == 2, 1, 0),
    divorced_missing = ifelse(as.numeric(divorced_fac) == 3, 1, 0),
    no_move = ifelse(as.numeric(moving_fac) == 1, 1, 0),
    new_res = ifelse(as.numeric(moving_fac) == 2, 1, 0),
    new_mun = ifelse(as.numeric(moving_fac) == 3, 1, 0),
    move_mis = ifelse(as.numeric(moving_fac) == 4, 1, 0),
    female = ifelse(as.numeric(gender_fac) == 2, 1, 0),
    first_child_rec = ifelse(first_child == 1, 1, 0),
    first_child_missing = ifelse(first_child == 2, 1, 0),
    female_alter = ifelse(gender_alter_fac == "Female", 1, 0),
    male_alter = ifelse(gender_alter_fac == "Male", 1, 0),
    missing_gender_alter = ifelse(gender_alter_fac == "Missing", 1, 0)
  ) %>%
  select(
    dropped,
    dyad_educ_sim_cen,
    dyad_gender_sim_cen,
    dyad_age_sim_cen,
    dyad_ethnicity_sim_cen,
    avsim_alter_educ_cen,
    avsim_alter_age_cen,
    ei_alter_gender_rev_cen,
    ei_alter_ethnicity_rev_cen,
    not_dear,
    dear,
    not_asked,
    degree_cen,
    educ_ego_cen,
    age_cen,
    female,
    no_mig,
    nonwestern_mig,
    western_mig,
    divorced,
    new_res,
    new_mun,
    first_child_rec,
    educ_alter_cen,
    age_alter_cen,
    female_alter,
    no_mig_a,
    nonwestern_mig_a,
    western_mig_a,
    coll,
    samegroup,
    neighbour,
    friend,
    advisor,
    otherrel,
    times_dropped_earlier_cen,
    rel_a_b3,
    rel_a_36,
    rel_a_o6,
    net_density_cen,
    size_cen,
    censor
  ) %>%
  psych::describe() %>%
  mutate(
    name = c(
      "Dropped",
      "Dyadic similarity: education",
      "Dyadic similarity: gender",
      "Dyadic similarity: age",
      "Dyadic similarity: ethnicity",
      "Confidant uniqueness education",
      "Confidant uniquenessy age",
      "Confidant uniqueness gender",
      "Confidant uniqueness ethnicity",
      "Confidant is not dear",
      "Confidant is dear",
      "Closeness not asked",
      "Embeddedness",
      "Education ego",
      "Age",
      "Female",
      "No migration background",
      "Non-western migration background",
      "Western migration background",
      "Divorced (ref. not)",
      "New residence (ref. no move)",
      "New municipality",
      "First child born",
      "Education alter",
      "Age alter",
      "Alter is female",
      "No migration background confidant ",
      "Non-western migration background confidant",
      "Western migration background confidant",
      "Colleague",
      "Same group or club",
      "Neighbour",
      "Friend",
      "Advisor",
      "Other relation",
      "Times dropped earlier",
      "Knows confidant for < 3 years",
      "Knows confidant for 3-6 years",
      "Knows confidant  > 6 years",
      "Net density",
      "Net size",
      "Censored"
    )
  ) %>%
  select(name, n, mean, sd, median, min, max)

desstats_table %>%
  kbl(caption = "Table 1. Descriptive statistics of discrete time hazard models 1-6",
      digits = 3,
      row.names = F) %>%
  kable_classic(
    full_width = F,
    bootstrap_options = c("hover", "condensed"),
    fixed_thead = T
  )

Table 1. Descriptive statistics of discrete time hazard models 1-6

name	n	mean	sd	median	min	max
Dropped	49449	0.643	0.479	1.000	0.000	1.000
Dyadic similarity: education	49449	0.000	1.000	0.364	-4.982	0.850
Dyadic similarity: gender	49449	0.000	1.000	0.459	-2.184	0.459
Dyadic similarity: age	49449	0.000	1.000	-0.008	-8.310	0.747
Dyadic similarity: ethnicity	49449	0.000	1.000	0.420	-2.542	0.420
Confidant uniqueness education	49449	0.000	1.000	0.000	-6.311	1.271
Confidant uniquenessy age	49449	0.000	1.000	0.097	-7.208	1.344
Confidant uniqueness gender	49449	0.000	1.000	0.144	-2.084	1.258
Confidant uniqueness ethnicity	49449	0.000	1.000	0.398	-3.840	0.398
Confidant is not dear	49449	0.249	0.432	0.000	0.000	1.000
Confidant is dear	49449	0.106	0.308	0.000	0.000	1.000
Closeness not asked	49449	0.645	0.479	1.000	0.000	1.000
Embeddedness	49449	0.000	1.000	-0.229	-1.791	1.332
Education ego	49449	0.000	1.000	-0.202	-2.782	1.346
Age	49449	0.000	1.000	0.042	-1.722	3.115
Female	49449	0.567	0.496	1.000	0.000	1.000
No migration background	49449	0.817	0.387	1.000	0.000	1.000
Non-western migration background	49449	0.045	0.208	0.000	0.000	1.000
Western migration background	49449	0.080	0.272	0.000	0.000	1.000
Divorced (ref. not)	49449	0.023	0.149	0.000	0.000	1.000
New residence (ref. no move)	49449	0.019	0.135	0.000	0.000	1.000
New municipality	49449	0.009	0.096	0.000	0.000	1.000
First child born	49449	0.003	0.055	0.000	0.000	1.000
Education alter	49449	0.000	1.000	-0.287	-3.081	1.389
Age alter	49449	0.000	1.000	-0.072	-1.889	1.744
Alter is female	49449	0.590	0.492	1.000	0.000	1.000
No migration background confidant	49449	0.918	0.274	1.000	0.000	1.000
Non-western migration background confidant	49449	0.047	0.212	0.000	0.000	1.000
Western migration background confidant	49449	0.029	0.167	0.000	0.000	1.000
Colleague	49449	0.094	0.291	0.000	0.000	1.000
Same group or club	49449	0.045	0.206	0.000	0.000	1.000
Neighbour	49449	0.059	0.235	0.000	0.000	1.000
Friend	49449	0.753	0.431	1.000	0.000	1.000
Advisor	49449	0.010	0.101	0.000	0.000	1.000
Other relation	49449	0.037	0.190	0.000	0.000	1.000
Times dropped earlier	49449	0.000	1.000	-0.384	-0.384	8.772
Knows confidant for < 3 years	49449	0.116	0.320	0.000	0.000	1.000
Knows confidant for 3-6 years	49449	0.175	0.380	0.000	0.000	1.000
Knows confidant > 6 years	49449	0.701	0.458	1.000	0.000	1.000
Net density	49449	0.000	1.000	0.275	-2.714	0.873
Net size	49449	0.000	1.000	0.762	-2.824	0.762
Censored	49449	0.158	0.365	0.000	0.000	1.000

Describing confidant loss

Life table

Recreate a life-table with the survival package. This is a KM fit, from which we can create a graphical representation of the survival and hazard function.

#extract number of dyads, ego, and dyad spells
dyad_ids <- unique(MyData$dyad_id)
ego_ids <- unique(MyData$nomem_encr)
process_ids <- unique(MyData$process_id)

#create survival data to use with surcfit. 
survival_data <- MyData %>%
  group_by(process_id) %>%
  filter(time == max(time)) %>%
  ungroup()

#estimate KM 
km_fit <- survfit(Surv(time, 1-censor) ~ 1, data=survival_data, se.fit = T)

#life table
km_fit %>%
  tidy() %>%
  select(1:5) %>%
  mutate(hazard = n.event / n.risk,
         time = time) %>%
  rename(period = time,
         survival = estimate) %>%
  kbl(caption = "Table 1. Life table",
      digits = 3,
      row.names = F) %>%
  kable_classic(
    full_width = F,
    bootstrap_options = c("hover", "condensed"),
    fixed_thead = T
  )

Table 1. Life table

period	n.risk	n.event	n.censor	survival	hazard
1	35526	26170	2105	0.263	0.737
2	7251	3489	696	0.137	0.481
3	3066	1156	363	0.085	0.377
4	1547	484	197	0.058	0.313
5	866	235	107	0.043	0.271
6	524	121	89	0.033	0.231
7	314	73	44	0.025	0.232
8	197	49	47	0.019	0.249
9	101	20	24	0.015	0.198
10	57	10	47	0.012	0.175

#export life table for office
life_table <- km_fit %>%
  tidy() %>%
  select(1:5) %>%
  mutate(hazard = n.event / n.risk,
         time = time) %>%
  rename(period = time,
         survival = estimate) 

Histogram of confidant loss

Recreate the histogram of confidant loss. These show the number of observations per wave and also a presentation of a random set of dyad spells.

survival_hist <- survival_data %>%
  mutate(censor  = factor(
    censor,
    levels = 0:1,
    labels = c("Lossed", "Censored")
  )) %>%
  ggplot(aes(x = time, fill = as.factor(censor))) +
  geom_histogram(binwidth = 1,
                     alpha = 0.8) + 
  scale_x_continuous(breaks = 1:10) +
  scale_fill_manual(values = c("#1b9e77",
                               "#d95f02")) +
  theme(
    panel.background = element_rect(fill = "#FFFFFF",
                                        colour = "black"),
    plot.background = element_rect(fill = "#FFFFFF"),
    panel.grid = element_line(colour = "grey"),
    panel.grid.major.x = element_blank(),
    text = element_text(family = "sans", size = 12),
    axis.title.x = element_text(hjust = 0.9, face = "bold"),
    axis.text.x = element_text(),
    axis.line = element_blank(),
    axis.title.y = element_text(hjust = 0.9, face = "bold"),
    axis.ticks = element_blank(),
    strip.background = element_rect(fill = "#A9A9A9"),
    panel.grid.minor = element_blank(),
    legend.position = "right",
    legend.title = element_blank(),
    legend.background = element_rect(fill = "#FFFFFF"),
    legend.key = element_rect(fill = "#FFFFFF")
  ) +
  labs(x = "Period", y = "Count")

#
set.seed(2023)

#Did not include this figure in the text
survival_censor_bar <- survival_data %>%
  sample_n(25) %>%
  mutate(censor  = factor(
    censor,
    levels = 0:1,
    labels = c("dissolved", "censored")
  )) %>%
  ggplot(aes(process_id, time)) +
  geom_bar(stat = "identity", width = 0.5) +
  geom_point(aes(
    process_id,
    time,
    color = as.factor(censor),
    shape = as.factor(censor)
  ),
  size = 4) +
  coord_flip() +
  scale_y_continuous(limit = c(0, 10), breaks = 1:10) +
  scale_color_viridis(discrete = T,
                      alpha = 0.9,
                      option = "D") +
  theme(
    panel.background = element_rect(fill = "#FFFFFF"),
    plot.background = element_rect(fill = "#FFFFFF"),
    panel.grid = element_line(colour = "grey"),
    panel.grid.major.y = element_blank(),
    panel.grid.minor.y = element_blank(),
    panel.grid.major.x = element_blank(),
    text = element_text(family = "sans", size = 12),
    axis.title.x = element_text(hjust = 0.9, face = "bold"),
    axis.text.x = element_text(),
    axis.line = element_blank(),
    axis.title.y = element_text(hjust = 0.9, face = "bold"),
    axis.ticks = element_blank(),
    strip.background = element_rect(fill = "#A9A9A9"),
    panel.grid.minor = element_blank(),
    legend.position = "top",
    legend.title = element_blank(),
    legend.background = element_rect(fill = "#FFFFFF"),
    legend.key = element_rect(fill = "#FFFFFF")
  ) +
  labs(y = "Period", x = "Dyad Spell ID")

# save in object
surv_desstats_1 <- survival_hist

ggsave(surv_desstats_1,
       file = "plots/results/survival/surv_desstats_1.jpg",
       width = 4,
       height = 3,
       dpi = 320)

# show graph
surv_desstats_1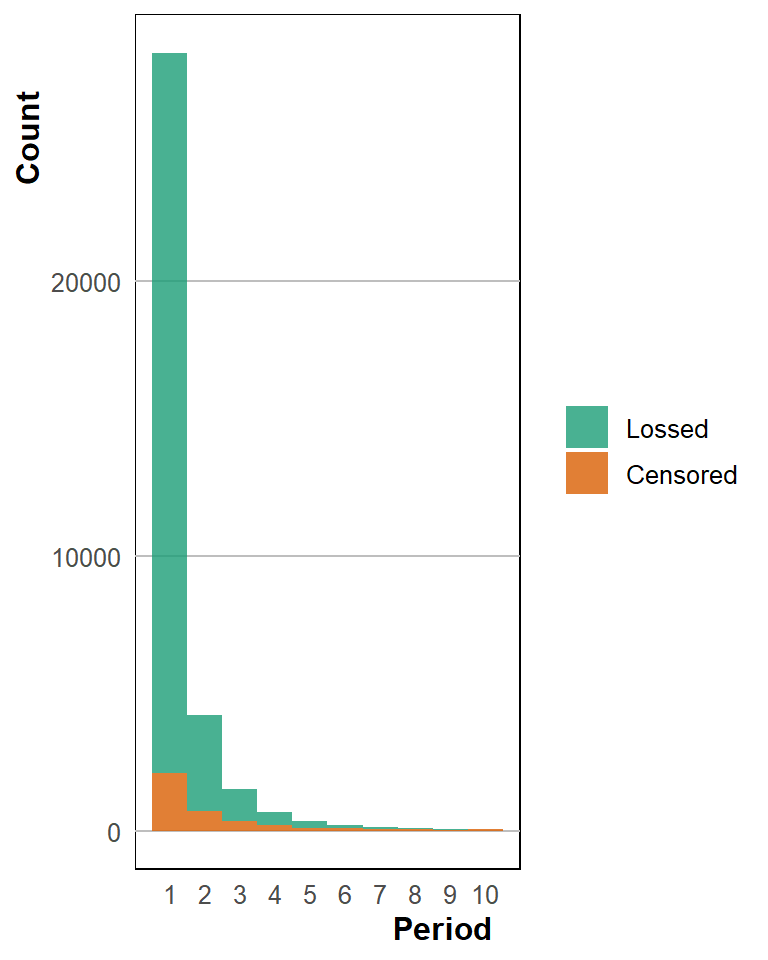

Count repeating dyads

Number of repeating dyads. First bit of code is used to calculate the % of dyads that only last for one spell (of one period). Second bit of code creates a bar chart with the number of dyads that have X dyad spells, which shows that the maximum number of dyad spells that a dyad can have is four.

MyData %>%
  select(dyad_id,
         nomem_encr,
         process_id,
         time,
         times_dropped_earlier,
         censor,
         dropped) %>%
  filter(censor == 0) %>%
  group_by(dyad_id, process_id) %>%
  summarise(n_process_id = n()) %>%
  ungroup() %>%
  group_by(dyad_id) %>%
  mutate(n_dyad_id = n()) %>%
  ungroup() %>%
  mutate(lost_period1 = n_process_id == n_dyad_id) %>%
  group_by(lost_period1) %>%
  summarise(n()) %>%
  transpose() %>%
  filter(row_number() == 2) %>%
  mutate(prop_dropped_period1 = (V2 / (V2 + V1)) * 100) %>%
  pull(prop_dropped_period1)

[1] 68.96281

spells_plot <- MyData %>%
  select(dyad_id,
         nomem_encr,
         process_id,
         time,
         times_dropped_earlier,
         censor,
         dropped) %>%
  filter(censor == 0) %>%
  group_by(dyad_id) %>%
  summarise(max_time_dropped = max(times_dropped_earlier) + 1) %>%
  ungroup() %>%
  group_by(max_time_dropped) %>%
  ggplot(aes(x = max_time_dropped, fill = max_time_dropped)) +
  geom_histogram(binwidth = 1,
                 alpha = 0.6) +
  stat_bin(binwidth = 1,
           geom = "text",
           aes(label = ..count..),
           vjust = -0.6) +
  scale_x_continuous(breaks = 1:4) +
  scale_fill_viridis(discrete = T,
                     alpha = 0.8,
                     option = "E") +
  theme(
    panel.background = element_rect(fill = "#FFFFFF"),
    plot.background = element_rect(fill = "#FFFFFF"),
    panel.grid = element_line(colour = "grey"),
    text = element_text(family = "sans", size = 12),
    axis.title.x = element_text(hjust = 0.9, face = "bold"),
    axis.text.x = element_text(),
    axis.line = element_blank(),
    axis.title.y = element_text(hjust = 0.9, face = "bold"),
    axis.ticks = element_blank(),
    strip.background = element_rect(fill = "#A9A9A9"),
    panel.grid.minor = element_blank(),
    legend.position = "none",
    legend.title = element_blank(),
    legend.background = element_rect(fill = "#FFFFFF"),
    legend.key = element_rect(fill = "#FFFFFF")
  ) +
  labs(x = "#spells", y = "Count")

spells_plot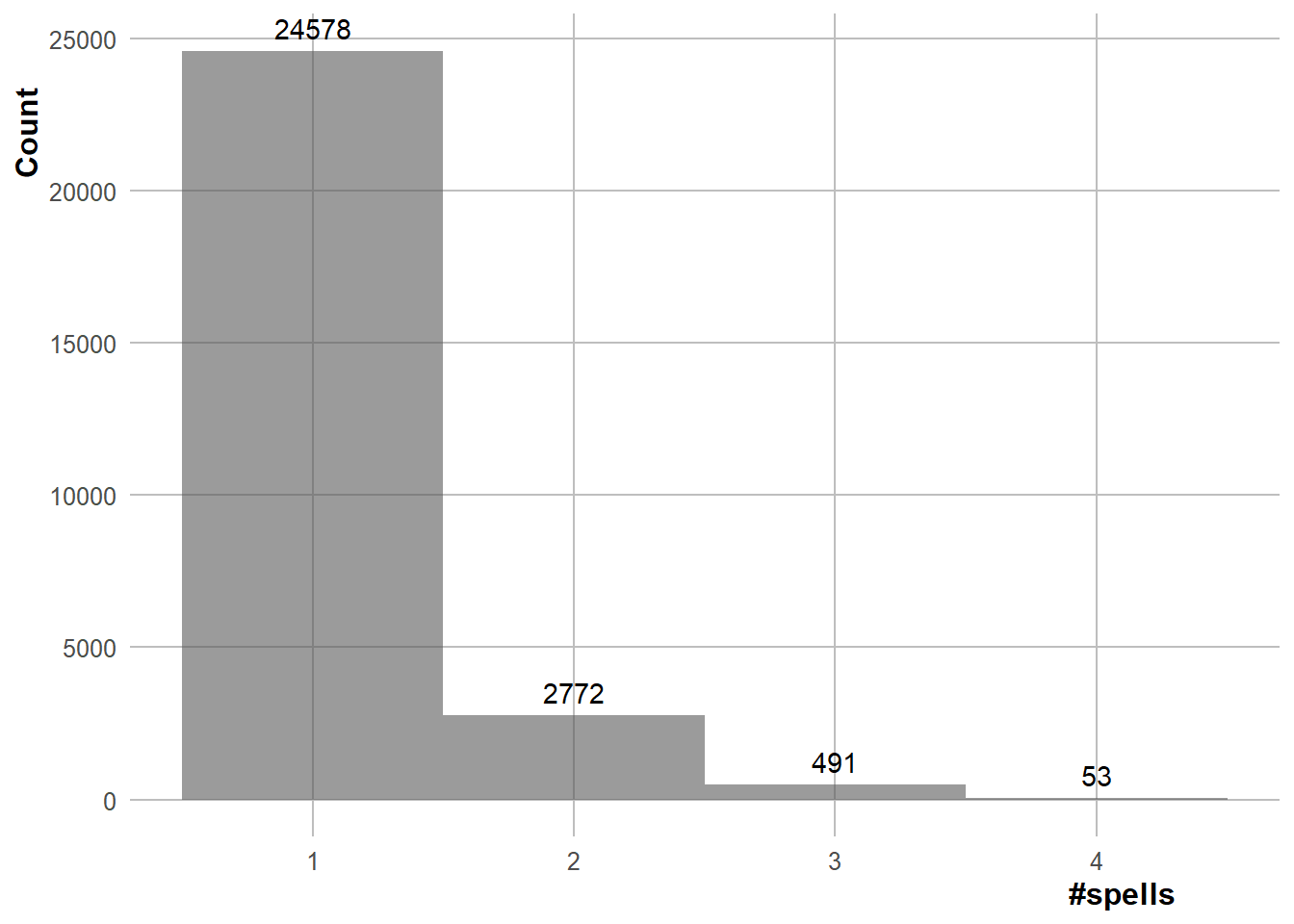

Survival and hazard graph

Recreate the survival and hazard graph.

surv_fig <- km_fit %>%
  tidy() %>%
  mutate(Hazard = n.event / n.risk,
         Survival = estimate,
         time = time) %>%
  pivot_longer(c(Survival, Hazard),
               values_to = "value",
               names_to = "surv_function") %>%
  ggplot(
    aes(
      x = time,
      y = value,
      colour = surv_function,
      shape = surv_function,
      fill = surv_function
    )
  ) +
  #geom_point(size = 2.5) +
  geom_line() +
  geom_area(alpha = 0.6) +
  facet_wrap(vars(surv_function)) +
  labs(x = "Period", y = "Probability") +
  scale_x_continuous(breaks = 1:10) +
  scale_fill_manual(values = c("#1b9e77",
                               "#d95f02")) +
  scale_colour_manual(values = c("#1b9e77",
                                 "#d95f02")) +
  theme(
    panel.background = element_rect(fill = "#FFFFFF",
                                        colour = "black"),
    plot.background = element_rect(fill = "#FFFFFF"),
    panel.grid = element_line(colour = "grey"),
    panel.grid.major.x = element_blank(),
    text = element_text(family = "sans", size = 12),
    axis.title.x = element_text(hjust = 0.9, face = "bold"),
    axis.text.x = element_text(),
    axis.line = element_blank(),
    axis.title.y = element_text(hjust = 0.9, face = "bold"),
    axis.ticks = element_blank(),
        strip.background = element_rect(fill = "#A9A9A9",
                                        colour = "black"),
    panel.grid.minor = element_blank(),
    legend.position = "none",
    legend.title = element_blank(),
    legend.background = element_rect(fill = "#FFFFFF"),
    legend.key = element_rect(fill = "#FFFFFF")
  )

#save results
ggsave(surv_fig, 
       file = "plots/results/survival/surv_fig.jpg",
       dpi = 320, 
       width = 5, 
       height = 3.5)

#show plot
surv_fig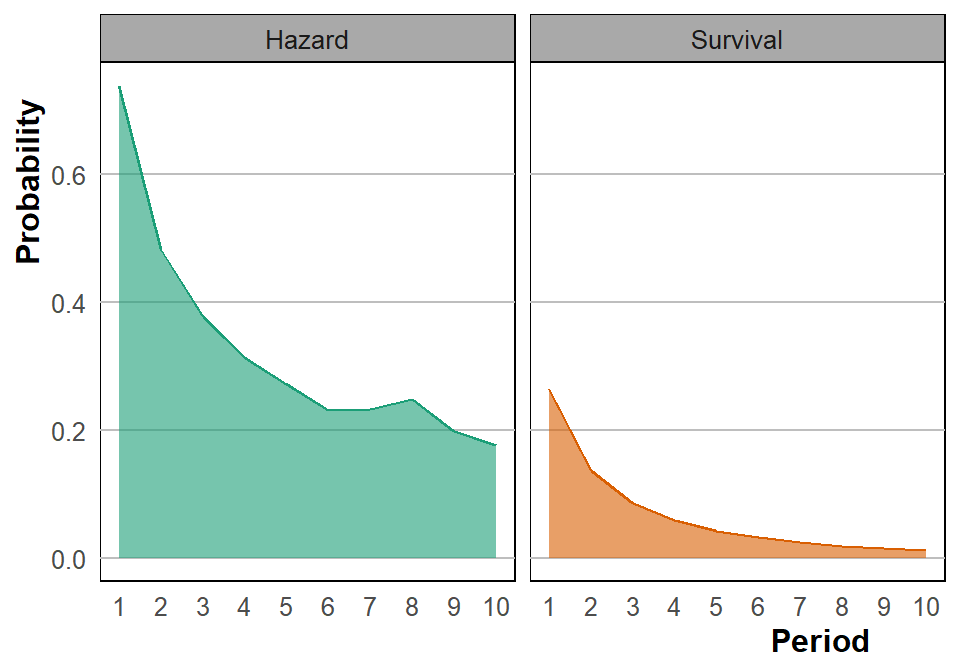

Dyadic similarity and confidant heterogeneity plots

Dyadic similarity plots

For similar and dissimilar dyads we estimate the survival function Subsequently we plot these in a figure.

Data preperation

Create a plot datafile.

#educ
km_fit_educ_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_educ_sim == 1), data=survival_data, se.fit = T)
km_fit_educ_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_educ_sim < 1), data=survival_data, se.fit = T)

educ_low <- km_fit_educ_sim_low %>%
  tidy() %>%
  select(1:5,7,8)  %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Dissimilar") %>%
  rename(period = time,
         survival = estimate)

educ_high <- km_fit_educ_sim_high %>%
  tidy() %>%
  select(1:5,7,8)  %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Similar") %>%
  rename(period = time,
         survival = estimate)

educ_df <- rbind(educ_high, educ_low) %>% 
  mutate(var = "Education")

#gender 
km_fit_gender_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_gender_sim == 1), data=survival_data, se.fit = T)
km_fit_gender_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_gender_sim == 0), data=survival_data, se.fit = T)


gender_low <- km_fit_gender_sim_low %>%
  tidy() %>%
  select(1:5,7,8)  %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Dissimilar") %>%
  rename(period = time,
         survival = estimate)

gender_high <- km_fit_gender_sim_high %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Similar") %>%
  rename(period = time,
         survival = estimate)

gender_df <- rbind(gender_low, gender_high) %>% 
  mutate(var = "Gender")

#ethncity 
km_fit_ethncity_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_ethnicity_sim == 1), data=survival_data, se.fit = T)
km_fit_ethncity_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_ethnicity_sim == 0), data=survival_data, se.fit = T)


ethnicity_low <- km_fit_ethncity_sim_low %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Dissimilar") %>%
  rename(period = time,
         survival = estimate)

ethnicity_high <- km_fit_ethncity_sim_high %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Similar") %>%
  rename(period = time,
         survival = estimate)

ethnicity_df <- rbind(ethnicity_low, ethnicity_high) %>% 
  mutate(var = "Migration background")

#age
km_fit_age_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_age_sim == 1), data=survival_data, se.fit = T)
km_fit_age_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (dyad_age_sim < 1), data=survival_data, se.fit = T)

age_low <- km_fit_age_sim_low %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Dissimilar") %>%
  rename(period = time,
         survival = estimate)

age_high <- km_fit_age_sim_high %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Similar") %>%
  rename(period = time,
         survival = estimate)

age_df <- rbind(age_low, age_high) %>% 
  mutate(var = "Age")

#plot
plot_df <- rbind(gender_df, age_df, educ_df, ethnicity_df)

Plot

Create a multipanel plot.

dyadic_sim <- plot_df %>%
  ggplot(aes(
    x = period,
    y = survival,
    colour = sim,
    fill = sim
  )) +
  geom_ribbon(aes(ymin = conf.low, ymax = conf.high),
              alpha = 0.4,
              linetype = "blank") +
  geom_line() +
  facet_wrap(vars(var)) +
  labs(x = "Period", y = "Survival function") +
  scale_x_continuous(breaks = 1:10) +
  scale_y_continuous(limits = c(0, 0.35),
                     breaks = c(0, 0.10, 0.20, 0.30)) +
  scale_fill_manual(values = c("#1b9e77",
                               "#d95f02")) +
  scale_colour_manual(values = c("#1b9e77",
                                 "#d95f02")) +
  theme(
    panel.background = element_rect(fill = "#FFFFFF",
                                    colour = "black"),
    plot.background = element_rect(fill = "#FFFFFF"),
    panel.grid = element_line(colour = "grey"),
    panel.grid.major.x = element_blank(),
    text = element_text(family = "sans", size = 12),
    axis.title.x = element_text(hjust = 0.9, face = "bold"),
    axis.text.x = element_text(),
    axis.line = element_blank(),
    axis.title.y = element_text(hjust = 0.9, face = "bold"),
    axis.ticks = element_blank(),
    strip.background = element_rect(fill = "#A9A9A9",
                                    colour = "black"),
    panel.grid.minor = element_blank(),
    legend.position = "bottom",
    legend.title = element_blank(),
    legend.background = element_rect(fill = "#FFFFFF"),
    legend.key = element_rect(fill = "#FFFFFF")
  )

# save dyadic sim plot
ggsave(dyadic_sim, file = "plots/results/survival/dyad_sim_surv.jpg", 
       dpi = 320,
       width = 6, 
       height = 6)

#show plot
dyadic_sim

Confidant heterogeneity plots

For homogeneous and heterogeneous dyads we estimate the hazard function. Subsequently we plot these different graphs.

Data preperation

Create a plot datafile.

#educ
km_fit_educ_conf_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (avsim_alter_educ == 1), data=survival_data, se.fit = T)
km_fit_educ_conf_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (avsim_alter_educ < 1), data=survival_data, se.fit = T)

educ_low <- km_fit_educ_conf_sim_low %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Unique") %>%
  rename(period = time,
         survival = estimate)

educ_high <- km_fit_educ_conf_sim_high %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Common") %>%
  rename(period = time,
         survival = estimate)

educ_conf_df <- rbind(educ_high, educ_low) %>% 
  mutate(var = "Education")

#gender 
km_fit_gender_conf_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (ei_alter_gender_rev == 1), data=survival_data, se.fit = T)
km_fit_gender_conf_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (ei_alter_gender_rev < 0), data=survival_data, se.fit = T)


gender_low <- km_fit_gender_conf_sim_low %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Unique") %>%
  rename(period = time,
         survival = estimate)

gender_high <- km_fit_gender_conf_sim_high %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Common") %>%
  rename(period = time,
         survival = estimate)

gender_conf_df <- rbind(gender_low, gender_high) %>% 
  mutate(var = "Gender")

#ethnicity 
km_fit_ethnicity_conf_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (ei_alter_ethnicity_rev == 1), data=survival_data, se.fit = T)
km_fit_ethnicity_conf_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (ei_alter_ethnicity_rev  < 0), data=survival_data, se.fit = T)


ethnicity_low <- km_fit_ethnicity_conf_sim_low %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Unique") %>%
  rename(period = time,
         survival = estimate)

ethnicity_high <- km_fit_ethnicity_conf_sim_high %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Common") %>%
  rename(period = time,
         survival = estimate)

ethnicity_conf_df <- rbind(ethnicity_low, ethnicity_high) %>% 
  mutate(var = "Migration background")

#age
km_fit_age_conf_sim_high <- survfit(Surv(time, 1-censor) ~ 1, subset = (avsim_alter_age == 1), data=survival_data, se.fit = T)
km_fit_age_conf_sim_low <- survfit(Surv(time, 1-censor) ~ 1, subset = (avsim_alter_age < 1), data=survival_data, se.fit = T)

age_low <- km_fit_age_conf_sim_low %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Unique") %>%
  rename(period = time,
         survival = estimate)

age_high <- km_fit_age_conf_sim_high %>%
  tidy() %>%
  select(1:5,7,8) %>% 
  mutate(hazard = n.event / n.risk,
         sim = "Common") %>%
  rename(period = time,
         survival = estimate)

age_conf_df <- rbind(age_high, age_low) %>% 
  mutate(var = "Age")

#plot
plot_conf_df <- rbind(gender_conf_df, age_conf_df, educ_conf_df, ethnicity_conf_df)

Plot

Create a multipanel plot.

conf_sim <- plot_conf_df %>%
   ggplot(aes(
    x = period,
    y = survival,
    colour = fct_rev(as.factor(sim)),
    fill = fct_rev(as.factor(sim))
  )) +
  geom_ribbon(aes(ymin = conf.low, ymax = conf.high),
                alpha = 0.4, 
                color = "black",
              linetype = "blank") +
  geom_line() +
  facet_wrap(vars(var)) +
  labs(x = "Period", y = "Survival function") +
  scale_x_continuous(breaks = 1:10) +
  scale_y_continuous(limits = c(0, 0.35),
                     breaks = c(0,0.10,0.20,0.30)) +
  scale_fill_manual(values = c("#1b9e77",
                               "#d95f02")) +
  scale_colour_manual(values = c("#1b9e77",
                               "#d95f02")) +
  theme(
    panel.background = element_rect(fill = "#FFFFFF",
                                        colour = "black"),
    plot.background = element_rect(fill = "#FFFFFF"),
    panel.grid = element_line(colour = "grey"),
    panel.grid.major.x = element_blank(),
    text = element_text(family = "sans", size = 12),
    axis.title.x = element_text(hjust = 0.9, face = "bold"),
    axis.text.x = element_text(),
    axis.line = element_blank(),
    axis.title.y = element_text(hjust = 0.9, face = "bold"),
    axis.ticks = element_blank(),
            strip.background = element_rect(fill = "#A9A9A9",
                                        colour = "black"),
    panel.grid.minor = element_blank(),
    legend.position = "bottom",
    legend.title = element_blank(),
    legend.background = element_rect(fill = "#FFFFFF"),
    legend.key = element_rect(fill = "#FFFFFF")
  )

#save plot
ggsave(conf_sim, 
       file = "plots/results/survival/conf_sim_surv.jpg",
       dpi = 320, 
       width = 6,
       height = 6)

#show plot
conf_sim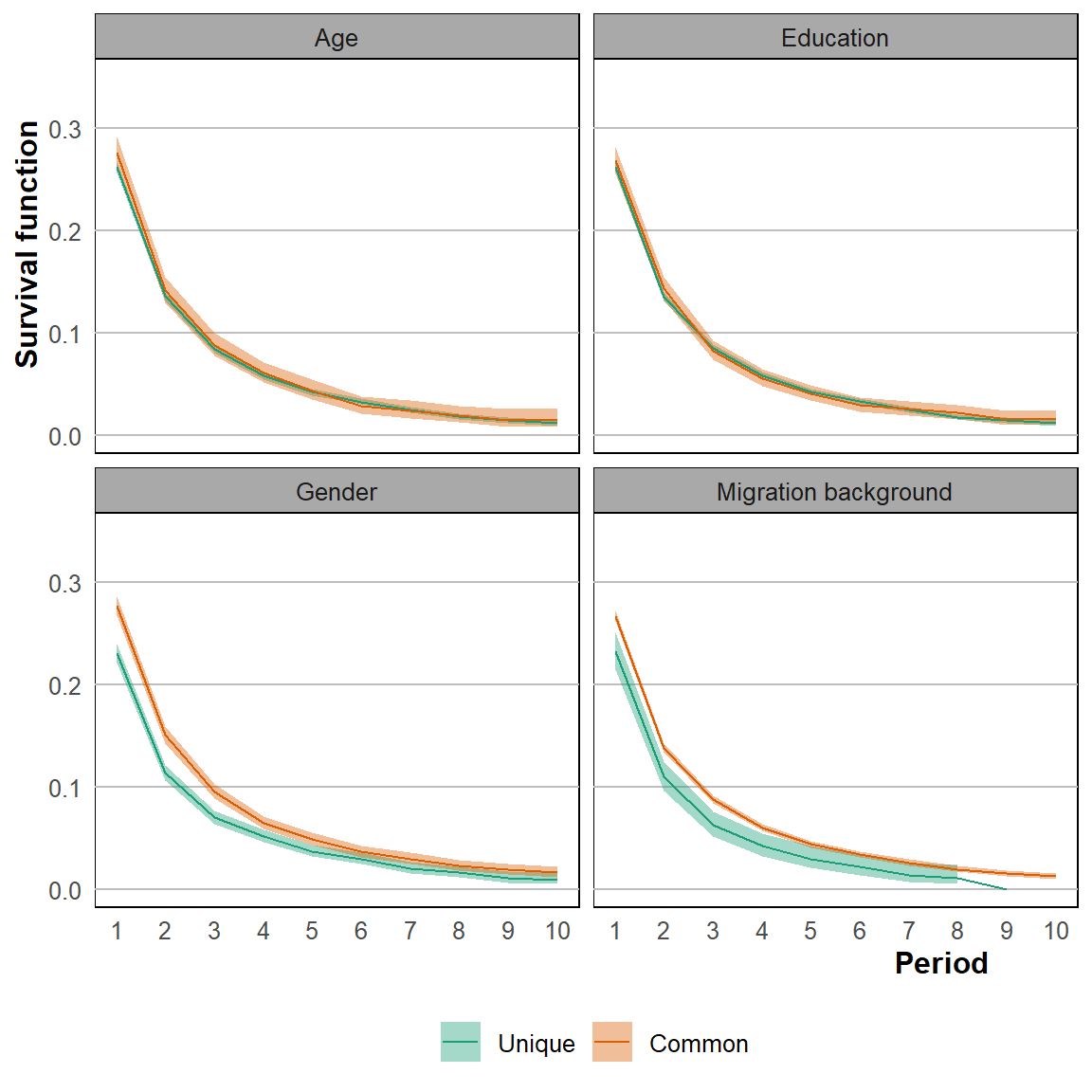

---

Copyright © 2023 Jeroense Thijmen